int按位赋值给float

起因#

调试ADC测电压时候，读到的uint16_t数值为1507，转换后得到的电压为1.2V。当时以为是uint16_t按位赋值给float类型数据得到的1.2V。
当时特意写了一个函数测试，int按位赋值给float，结果编译器报错。然后用浮点数转换器发现值又对不上。接着又把int强转float和按位赋值搞混淆。

结论#

1. 由公式1507* 3.3 / 4095 = 1.2。ADC分辨率为12位，支持的输出范围2^12 - 1 = 4095，参考电压为3.3V。
2. 强转只是尽量保证数值不变。
3. printf输出不会按格式控制符自动强转数据类型,若不符合所设格式的类型则输出0。
4. 格式控制符%x表示将整数值转换为十六进制表示。
5. 格式控制符%f和%lf的处理一致，都是输出精确到小数点后6位。只为了编写更加规范。
6. %g 是 C 语言中的格式控制符，用于打印浮点数。它会根据浮点数的值自动选择 %f 或 %e（或 %E来打印，以产生更简洁和易读的输出。
   如果浮点数的绝对值小于 0.0001 或者大于等于 10^6，%g 将使用指数形式 %e（或 %E）打印。
   否则，%g 将使用定点形式 %f 打印，但会根据数字的精度进行调整，以确保输出的有效数字位数不超过所需的精度。
7. int和float符号位都是在最高位。

   #include <stdint.h> #include <stdio.h> void main(void) { int i_a = 1507; float f_b = i_a; float f_c = 1507.0; int i_d = f_c; printf("i_a = %d\r", i_a); // 输出：i_a = 1507 printf("i_a = %f\r", i_a); // i_a = 0.000000 printf("i_a = %f\r", (float)i_a); // i_a = 1507.00000 printf("i_a = %x\r", (float)i_a); // i_a = 0 printf("f_b = %d\r", f_b); // f_b = 0 printf("f_b = %f\r", f_b); // f_b = 1507.000000 printf("f_c = %d\r", f_c); // f_c = 0 printf("f_c = %f\r", f_c); // f_c = 1507.000000 printf("i_d = %d\r", i_d); // i_d = 1507 printf("i_d = %f\r", i_d); // i_d = 0.000000 //ADC分辨率为12位2^12 - 1 = 4095 printf("vol = %d / 4095 * v_ref = %f", i_d, i_d * 3.3 / 4095 ); //vol = 1507 * v_ref / 4095 = 1.214432 }

浮点数回顾#

组成结构#

按IEEE754标准规定浮点数格式:

0.1 + 0.2 = ?#

连续的二进制数，对应的十进制数却是不连续的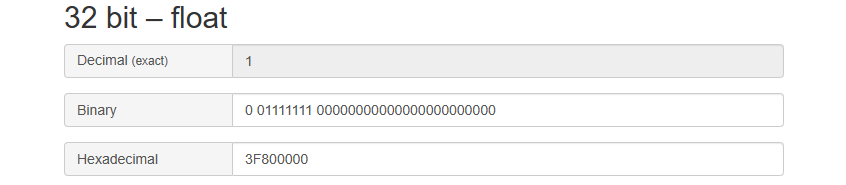

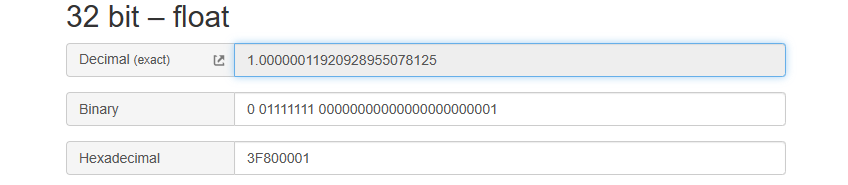
#include <stdio.h>

void main(void)
{
  float f_a = 0.1 + 0.2;
  double d_a = 0.1 + 0.2;

  printf("%f\n", f_a);         // 输出：0.300000
  printf("%.15f\r", f_a);      // 0.300000011920929
  printf("%d\n", sizeof(f_a)); // 4
  printf("%lf\n", d_a);        // 0.300000
  printf("%.15lf\r", d_a);     // 0.300000000000000
  printf("%d\n", sizeof(d_a)); // 8
}

normal number：指数位不全为0或1#

单精度浮点数范围：（-2^128, -2^-126] ⋃ [2^-126, 2^128)
有隐藏位1：value = sign x 2 ^exp x (1 + fraction)
1:

最大正值：

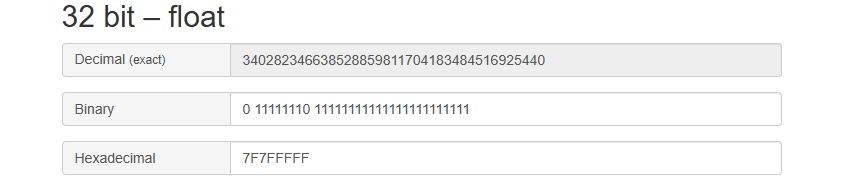
denormal number：：指数位全为0#

表示0和接近0的值
单精度浮点数范围：（-2^-126, 2^-126)
无隐藏位1：value = sign x 2^-126 x fraction
+0和-0：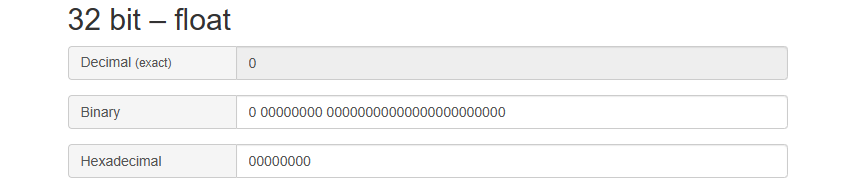


最小正值：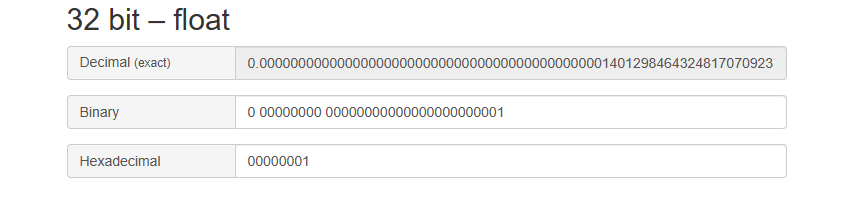

特殊值：指数位全为1#

无穷infinity：指数位全为1，尾数全为0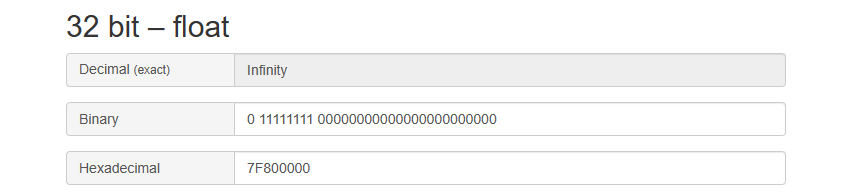

无效值NaN ：指数位全为1，尾数不全为0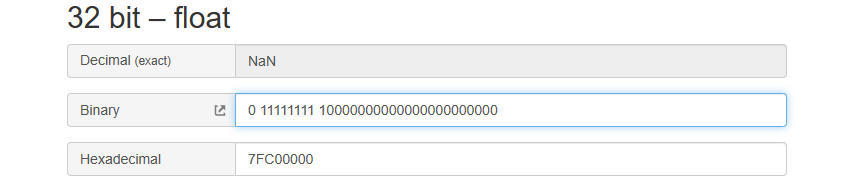

精确度，有效位数#

二进制有效位是换算到十进制的有效位：
float：2^23 = 8388608，共7位，就是说在二进制下能表示的准确的23位的数转换到十进制下最大的数是7位的，数值是多少不重要，因为这个数是在十进制下是7位，所以float在十进制下的精度位最多7位，但绝对能保证6位，float的精度为67位；
double：2^52 = 4503599627370496，共16位，double的精度为1516位。

参考#

IEEE 754 - 维基百科，自由的百科全书 (wikipedia.org)
15 张图带你深入理解浮点数 (studygolang.com)
深度理解IEEE754浮点数 | CS笔记 (pynote.net)
为什么单精度浮点数的精度是7位 (pkxpp.github.io)
float与double的范围和精度-腾讯云开发者社区-腾讯云 (tencent.com)
Base Convert: IEEE 754 Floating Point
IEEE-754 Floating Point representation explained (bartaz.github.io)